Suppose for all `x,y\inR` we have `f(x+y)=f(x)+f(y)+xy` and `f(4)=10`.
Let find the value of `f(2001)`
We will use this theorem to solve the following problem
For all `x,y\inR` we have `f(n+1)=f(n)+f(1)+n` then
`f(n+1)-f(n)=f(1)+n` we knew that: `\triangle``f(n)=f(n+1)-f(n)`
Then, `\sum_{n=0}^{2000}``\triangle``f(n)=f(2001)-f(0)`
Or `f(2001)=``\sum_{n=0}^{2000}``f(n+f(1))``+f(0)` `(*)`
As we had: `f(x+y)=f(x)+f(y)+xy` when `x=y=2` then, `f(4)=2f(2)+4`
`f(4)=10``\rightarrow``f(2)=3`
We play the same role to find `f(1)`
When `x=y=1` then, `f(2)=2f(1)+1``\rightarrow``f(1)=1`
As the same play, we will get `f(0)=0`
From the equation of `(*)` , therefore: `f(2001)=``\sum_{n=0}^{2000}``(n+1)``+f(0)`
`f(2001)=``\sum_{n=0}^{2000}``(n+1)``=(2000(2001))/2`
Solution by: Thin Sokkean

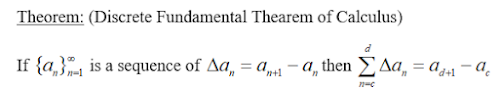

No comments:
Post a Comment